Systemic Risk in China’s Financial Industry Due to the COVID-19 Pandemic

I. Introduction

In this paper, we (a) test the impact of COVID-19 on the systemic risks of China’s financial industry, and (b) evaluate which industry experienced the largest fluctuations in systemic risks. Investigating both (a) and (b) are important because China’s financial system is not yet perfect, and the ability to prevent and resolve financial systemic risks caused by market emergencies needs to be improved (Bai & Shi, 2014). The outbreak of the COVID-19 pandemic has had a serious economic impact on China’s economy.^[1] The pandemic has also impacted the financial industry. In response, banks reduced credit demand and intermediary business, and overdue loans have increased. Moreover, sales of the insurance industry have been severely affected by the pandemic, and sales of traditional insurance types have fallen sharply. The securities industry has been affected by market sentiment, and trading volume, investment and financing activities have fluctuated greatly; see, for instance, Zuo (2020), Duan (2020), Ni et al. (2020).

According to Zuo (2020), the banking, insurance, and securities industries have become closely linked, and the comprehensive operation of various industries has also intensified the transmission of risks within the financial industry. Cross-contagion and superimposed resonance of risks may further induce financial systemic risks.

We use the CoVaR—the value at risk (VaR) of the financial system conditional on institutions being under distress. This method was proposed by Adrian & Brunnermeier (2016) and provides a way to measure the loss of investment portfolios of other financial markets or financial institutions under crisis or high-risk conditions. Adrian & Brunnermeier (2016) constructed CoVaR, Exposure-CoVaR, Network-CoVaR, and Forward-CoVaR based on the CoVaR method. These are a series of systemic risk measurement indicators based on risk spillover and tail dependence among financial institutions. Many studies (Bai & Shi, 2014) adopt new methods, such as the CoVaR and the Marginal Expected Shortfall-System Risk (MES-SRISK) to measure the systemic risk level of China’s financial institutions, assess the risk contribution of individual institutions, and monitor the dynamic changes of China’s systemic financial risks. Among these methods, the CoVaR method combined with the traditional VaR can more accurately capture the impact of a single financial institution’s risk on systemic risk, and it can also accurately measure the risk spillover effect in the financial network. Our contribution to the literature is through analyzing the effects of COVID-19 on systemic risk of the financial industry in China. This has not been done previously and nothing is understood on COVID-19 and the financial industry effects.

The remainder of this paper proceeds as follows. Section Ⅱ provides the research model and data. Section Ⅲ presents the empirical results. Section Ⅳ concludes this work.

II. Methodology and Data

A. Calculation of systemic financial risk

The paper first draws on the systemic risk indicator $\ {\mathrm{\Delta}CoVaR}_{q}^{system|\ i}$proposed by Adrian & Brunnermeier (2016) to calculate the systemic risk of financial institution i, where ${\mathrm{\Delta}CoVaR}_{q}^{system|\ i}$ indicates the contribution of financial institution i to the systemic risk of the financial system.

$$\begin{matrix} \Pr\left( X^{j} \leq CoVaR_{q}^{j|i} \middle| X^{i} = VaR_{q}^{\ i} \right) = q \hspace{25mm}(1) \\ \end{matrix}$$

$VaR_{q}^{\ i}$ is the VaR of institution i under the confidence level of q. $Pr(X^{i} \leq VaR_{q}^{i}) = q$ where $X^{i}$ represents the rate of return of institution i. $CoVaR_{q}^{j|i}$ represents the VaR of institution j when institution i is in crisis and the loss is $VaR_{q}^{\ i}.$ The contribution of a single financial institution i to the systemic risk of the financial institution j (or system) can be obtained as:

$$\begin{matrix} {\mathrm{\Delta}CoVaR}_{q}^{j|\ i} = CoVaR_{q}^{j|X^{i} = VaR_{q}^{i}} - CoVaR_{q}^{j|X^{i} = Median_{\ }^{i}} \hspace{3mm}(2)\\ \end{matrix}$$

According to definitions, contributions from individual financial institution i to the systemic risks of the financial system is derived:

$$\begin{matrix} {\mathrm{\Delta}CoVaR}_{q}^{system|\ i} \\ = CoVaR_{q}^{system|X^{i} = VaR_{q}^{i}} - CoVaR_{q}^{system|X^{i} = VaR_{\ }^{Median_{\ }^{i}}} \hspace{5mm}(3)\\ \end{matrix}$$

$Median_{\ }^{i}$ uses $VaR_{50\%}^{i}$, which represents the VaR of the financial institution i at the level of the 50% confidence interval. It represents the financial institution in a normal state. In this paper, the value of q is 95%, which is the 95% confidence interval.

Since financial data in reality is often not distributed normally but distributed with “high peak and fat tail”, in order to more accurately capture the relationship between different parts of the overall distribution, a quantile regression is introduced on this basis to form dynamic CoVaR. Quantile regression is a regression based on the different quantiles of variables and includes the state variable, $M_{t}$, to calculate the time series of the contribution of a single financial institution to the systemic risk.

Firstly, quantile regression is used to calculate the dynamic VaR of the financial institution i at the 95% and 50% confidence levels. The quantile regression equation form is:

$$\begin{matrix} X_{t}^{i} = \alpha^{i} + \gamma^{i}M_{t} + \varepsilon_{t}^{i} \hspace{50mm}(4) \\ \end{matrix}$$

$X_{t}^{i}$ represents the rate of return of institution i at time t, and $M_{t}$ is a state variable, which specifically covers three categories, namely liquidity risk, credit risk, stock market risk; see Table 1 for details.

Secondly, quantile regression is used to calculate the VaR of the financial system under the 95% confidence level when the financial institution i is under pressure and normal. The regression equation is as follows:

$$\begin{matrix} X_{t}^{system} = \alpha^{system|i} + \beta^{system|i}X_{t}^{i} + \gamma_{\ }^{system|i}M_{t} + \varepsilon_{t}^{system|i} \hspace{2mm}(5) \\ \end{matrix}$$

$X_{t}^{i}$ and $M_{t}$ have the same meanings as in Equation (4), $X_{t}^{system}$ is the rate of return of the financial system at time t, expressed as the logarithmic growth rate of each financial industry index. What needs to be pointed out is that when calculating systemic risks in different financial industries, the logarithmic growth rates of different financial indexes should be used; see Table 1 for details.

By regressing, we obtain the predicted value, so we can get:

$$\begin{matrix} VaR_{t}^{i}\left( q \right) = {\widehat{\alpha}}_{q}^{i} + {\widehat{\gamma}}_{q}^{i}M_{t} \hspace{54mm}(6) \\ \end{matrix}$$

$$\begin{matrix} CoVaR_{t}^{i}\left( q \right) = {\widehat{\alpha}}_{q}^{system|i} + {\widehat{\beta}}_{\ }^{system|i}VaR_{t}^{i}\left( q \right) + {\widehat{\gamma}}_{q}^{system|i}M_{t} \hspace{4mm}(7) \\ \end{matrix}$$

Then the contribution of a single financial institution to systemic risk ${\mathrm{\Delta}CoVaR}_{q}^{system|\ i}$ can be expressed as:

$$\begin{align} &\mathrm{\Delta}CoVaR_{t}^{system|i}\left( q \right) = CoVaR_{t}^{i}\left( q \right) - CoVaR_{t}^{i}\left( 50\% \right)\\ &= {\widehat{\beta}}^{system|i}\left( VaR_{t}^{i}\left( q \right) - VaR_{t}^{i}\left( 50\% \right) \right) \hspace{34mm}(8) \end{align}$$

After obtaining the contribution of each institution in the three industries to the systemic risks of financial institutions, it is necessary to finally calculate the systemic financial risks of the three industries over time, as:

$$\begin{matrix} \mathrm{\Delta}CoVaR_{t}^{system} = \sum_{}^{}{\frac{V_{i,t}}{V_{system,t}}\mathrm{\Delta}CoVaR_{t}^{system|i}} \hspace{25mm}(9) \\ \end{matrix}$$

Where $\mathrm{\Delta}CoVaR_{t}^{system}$ represents the systemic financial risk of a financial industry at time t; $\mathrm{\Delta}CoVaR_{t}^{system|i}$ represents the contribution value of financial institution i to the systemic risk of the financial industry at time t; $V_{i,t}$ represents the market value of institution i at time t, represented by the market value of equity on that day; $V_{system,t}$ represents the total market value of the industry in which institution i belongs at time t, and the ratio of the two is the weight of the industry in which institution i belongs.

B. Data Selection

This paper selects non-special-treatment companies in various industries that were listed as A shares before December 2019, including a total of 30 listed banking companies, 46 listed securities companies, and seven insurance companies (according to the new China Securities Regulatory Commission industry classification). The sample interval is from December 2, 2019 to May 31, 2020. The basic variables and related descriptive statistics used to calculate systemic risks (explained variables) in various financial industries are given in Table 1.

III. Results and Analysis

Section Ⅲ contains two parts of analysis. The first part analyzes the overall situation of systemic risks in the financial industry before and after the outbreak of the COVID-19 pandemic based on systemic risk data. The second part takes a comparative analysis of the systemic risk trends of the banking, securities, and insurance industries.

A. Overall analysis of systemic risks before and after the COVID-19 pandemic

Figure 1:Trends of systemic risk in various financial industries

The figure shows the trends of systemic risk in various financial industries between December 2019 to May 2020. Since $\mathrm{\Delta}CoVaR_{t}^{system}$ has positive and negative values, for simplicity, Figure 1 takes its absolute value to represent risk.

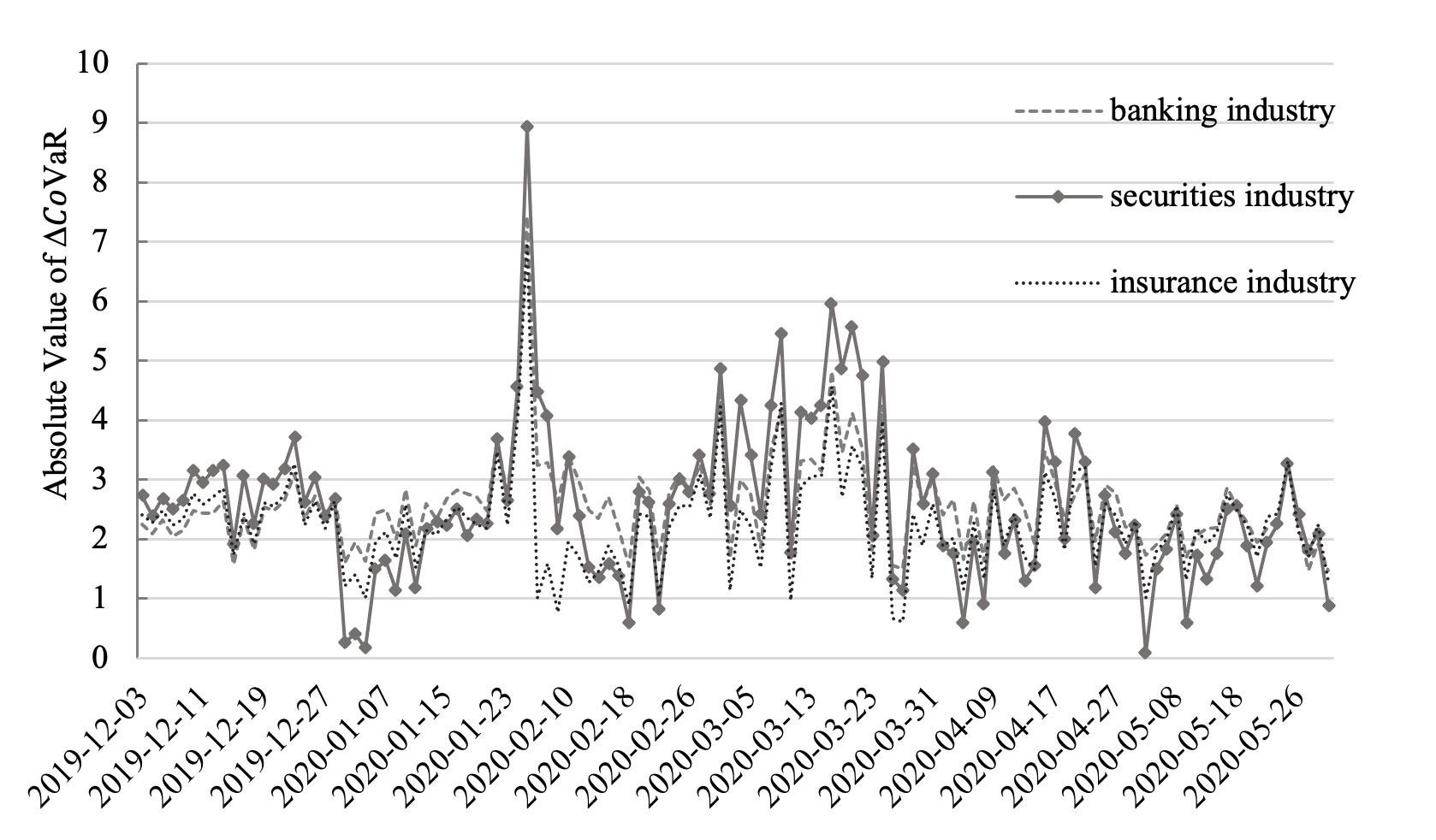
As Figure 1 shows, the larger the absolute value, the greater the institutional risk. It can be concluded from Figure 1 that the occurrence of COVID-19 has increased the volatility of systemic risks in the financial industry. Specifically, in December 2019, before the outbreak of COVID-19, the fluctuation in systemic risk was relatively stable. In February with the outbreak of COVID-19, the degree of fluctuation of systemic risk increased greatly. Since important news about COVID-19 was released during the holiday period (the Spring Festival), the information backlog caused a linear increase in systemic risks from the beginning of February. With the pandemic persisting post-February, the volatility of systemic risks was significantly higher than in December. Due to the uncertainty brought about by COVID-19, it has not only increased systemic financial risks, but also increased the volatility of systemic risks in the financial system.

B. Comparative analysis of systemic risk trends in three industries

As Figure 1 indicates, we can see that compared with banking and insurance industries, securities industry has greater systemic risks and higher volatility. The systemic changes in the banking and the insurance industries are similar, and the absolute value and the degree of volatility are relatively small compared to the securities industry. This shows that the pandemic has had a greater impact on securities in the financial industry. The securities industry has the highest contribution to systemic financial risks. There may be several reasons for this.

According to Wang et al. (2020), in China, the insurance industry has strong connections with the banking industry. In terms of business, the insurance industry cooperates with the banking sector to complete part of insurance sales. In terms of policies, the China Banking Regulatory Commission and the China Insurance Regulatory Commission have also merged into the China Banking Regulatory Commission. The business structure of the insurance industry is relatively simple, which leads to weak externalities of the insurance industry. Therefore, the systemic risk of this industry is relatively small compared to the banking and securities industries.

Compared with the banking and insurance industries, the securities industry is involved in a large number of derivative financial product transactions, which is risky. For example, the liquidation and settlement risks of derivative product transactions have greatly increased. At the same time, excessive speculation and high-risk investment speculation in the securities market has increased risks in the securities industry.

IV. Conclusion

In this paper, we start on exploring systemic risks on the financial industry motivated by the broader implications of the COVID-19 pandemic. Selecting daily data for 30 listed banking companies, 46 listed securities companies and seven insurance companies between December 2019 to May 2020, we apply the dynamic CoVaR method to measure changes in systemic risk in the financial industry during the COVID-19 pandemic. The results show that during the COVID-19 pandemic, the systemic financial risks of various financial industries increased significantly, and the degree of volatility also increased. We find that the impact of the COVID-19 pandemic on the systemic risks of the securities industry is greater than that of the banking and insurance industries. Therefore, policymakers should rationally guide the direction of capital investment in the securities industry.

Acknowledgements

Helpful comments and suggestions from a referee of this journal is acknowledged.